
In this article, I will mention only a few topics relevant to the violin acoustics. Please come back to this site from time to time to view other subjects. A systematic treatise will be published elsewhere.
First of all, let's look at the physiology of hearing. The primary sensing organ in the ear is the snail shaped cochlea. Inside the fluid filled cochlea are lined with specialized neurons called hair cells. The salient feature here is that the hair cell at a given location in the cochlea will only response to a vibration of a specific frequency. In other words, the incoming complex sound is frequency-analyzed into the component form (partials) by the cochlea. The cortex is in fact fed with the spectrum information. One of the component (the lowest frequency, or the highest intensity) gives us the sensation of pitch and the constitution of the spectrum, the timbre of the sound. In what follows, when I mention the "frequency" of a complex sound, I mean the frequency of this fundamental partial which gives us the feeling of pitch. Both pitch and color are human senses of vibration and electromagnetic wave, respectively of a specific frequency.

In addition to the absolute frequency sensing, there is another important quality which the auditory nerve system is capable of. It is the sensing of consonant sounds - the foundation of the musical scales. The occurrence of consonant sounds is based on the relative frequencies of two or a group of sounds. In simple physical terms, the consonance can be described as follows: when the RATIO of the frequencies (freq. of the fundamental) of two sounds is a SIMPLE DIGITAL RATIO, certain smoothness and pleasantness are felt. The following consonant sounds are listed in the order of pleasantness: unison (frequency ratio 1:1), octave (1:2), perfect 5th (2:3), perfect 4th (3:4), major 6th (3:5), major 3rd (4:5), minor 3rd (5:6), minor 6th (5:8), etc. As you can see that doubling the frequency means one octave. The octave is divided into smaller intervals. There are many ways to subdivide the octave. I will describe the major scale as an example below. The octave is divided into 7 intervals. I myself can never remember those fancy English names for the notes. (If I use the word "tonic" here, someone might think that I am talking about health foods!) Therefore, I'll use numbers to represent the 7 notes (1 being the key note). The intervals, represented by the frequency ratios, are shown in the brackets:
1 (8:9) 2 (9:10) 3 (15:16) 4 (8:9) 5 (9:10) 6 (8:9) 7 (15:16) 8
There are 3 different intervals in the above scale: major tone (8:9), minor tone (9:10), and semitone (15:16).
Since the intervals are represented by frequency ratios, the interval in the higher octave is therefore wider in the frequency difference than the corresponding interval in the lower octave. A violinist plays on the natural scales or the scales of just intonation as shown above.
When the condition for consonance is slightly off, one hears an unpleasant rattling sound. The best way to learn this is to listen the unison. If there is a slight difference in frequency, say df, one hears a third tone (called beat) whose frequency is df. Unlike a Tartini tone, the beat is a predominant sensation, any untrained ear should be able to hear it. The concept of beat should be explicitly and clearly taught to the beginning students (and their parents so they can tune their young children's violins at home). I now use tuning open A string as an example. Place the vibrating tuning forks near your ear and at the same time pluck the A string lightly. Listen to the pitches of both the forks and the A string. If the open A is not exactly 440 Hertz, say 437Hz (or 443Hz), you will hear a pulsating sound (i.e., beat) of 3 Hertz. Continue to tune the A string until the beat disappears. This is the most accurate way to tune the open A. I always have some doubt that human hearing could distinguish + - one Hertz, particularly at the higher octaves. As demonstrated above, it is possible to hear the perfect unison with the help of the beat frequency. In a group playing situation such as an orchestra, if some member is out of tune, the overall sound quality degrades due to the occurrence of beat. Once the unison sound is mastered, the rest of the consonant sounds will be much easier to learn.
The vibrations we hear every day are not "pure tone" (i.e., not a single frequency). A pure tone is generated by a sinewave generator. Similarly, a pure color light is generated by a laser device. Human hearing is a non-linear system. When a pure tone is impinged on the ear drum, a series of harmonics are also heard. This is the same as when you play A3 on the G-string, the open A-string will be vibrating due to the subharmonic excitation. A violin tone ideally should contain only the harmonic series. A violin string, in principle, only generate harmonic sounds. The sounds are composed of the fundamental frequency and the integer multiples of the fundamental frequency. Since the surface area of the string is small, therefore it will not emit audible sound. The vibration of the string is transmitted through the bridge to excite the violin body. The sound box has its own natural vibration modes. Therefore, a violin sound will contain predominantly the harmonic partials of the string plus the characteristic partials generated by the sound box. Certain strong partials outside the harmonic series may degrade the violin tone, particularly when you are playing the double stops. Producing a violin of relatively purer tone is one of the most challenging task in violin making.
The harmonics playing is a peculiar expressive facility for the instruments of the violin family. The harmonics in violins have the characteristic flute-like timbre. In principle, a harmonic is generated when the vibrating string length is subdivided into integer multiple of loops. The player's finger is placed lightly on one of the nodal point. The first harmonic is of course produced by dividing the string length into 2 loops. The player's finger is placed at the mid-length of the string to create a node there. Since the frequency is inversely proportional to the string length, half the length means double the frequency (i.e., one octave). The next one is to subdivide the string into 3 loops. Now there are 2 nodes. The lower register one is located approximately at the 3rd position, 2nd finger. This harmonic has 3 times the frequency of the open string. Remember a perfect 5th interval is 3/2, therefore, 3/1 is an octave higher 5th. The next harmonic is produced by dividing the string into 4 sections. 4 times the frequency means 2 octaves (i.e., double twice). There are 3 nodes. The lowest one is at 3rd position 1st finger. As mentioned earlier, the mid-point produces the stronger one-octave harmonic. Thus the 2-octave harmonic has only 2 practical nodes. The next is 5 loops (5 times the frequency). We have 4 nodal points. Remember the major 3rd interval is 5/4. Therefore, 5/1 is a 2-octave major 3rd. Let's take D-string for example. The major 3rd for open D is F#. The first node is at the F# location. Thus touch the string lightly at F# will produce 2-octave F#. The 2nd node is at the third position third finger (i.e., B). Try to find the other 2 nodal points. A node is almost a geometrical point. A cleaner harmonic is produced with the tip of your finger (minimum contact area) and bowing close to the bridge with less pressure and higher speed. What's about the higher harmonics with more than five loops? I leave it to the reader to figure them out. The 5-loop harmonic is just about the limit for the metal E-string. However, the lower strings are capable of producing higher harmonics. A violinist and composer should explore this further.
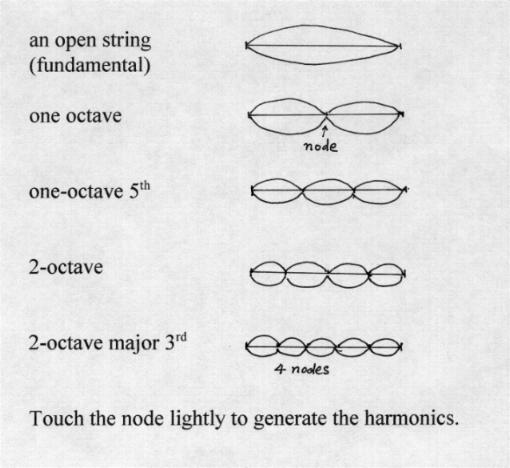
Since all the natural harmonics (i.e., the harmonics of the open string notes) are produced by lightly touching the strings, consequently, the pitches of the natural harmonics are slightly flatter than the corresponding notes produced by pressing the string all the way to the fingerboard. Pressing the string to the fingerboard increases the string tension. This is also the reason that the intervals on the fingerboard getting narrower at the higher register due to the increasing string height toward the bridge. (Another thing is about the imperfectness of the scale. I'll talk about this later.
The artificial harmonics are produced by using 2 fingers. One finger controls the free length of the string while the other touches the nodal point. For example, use the first finger to play the fundamental note and the 4th to touch the quarter point (of the free length) to generate the 2-octave harmonics. Extend the 4th finger one tone higher (i.e., the one-third point) to generate the one-octave perfect 5th. You can use either 1-3 or 2-4 finger to generate the two-octave major 3rd.
The above materials were drawn directly from my head and may contain errors and areas which may not be clear to the readers. Your comments and feedback are welcome.